Why Are There No Green Stars?

It’s a clear dark and Moonless night. You look skyward and see a cornucopia of twinkling lights – stars, some much brighter than the others, some faint enough to almost be invisible. Most of the stars appear white to your eye, but of the brighter ones a few have an obvious colored tint – perhaps a light blue or ruddy orange. If you were to pick up a pair of binoculars or a small telescope and scan the heavens you may fill in the spectrum a bit more, maybe some deeper reds, yellows, and more blues. But no greens*.

Why are there no green stars?  This is actually a common question and one that others have provided answers to elsewhere. (One of my favorite astronomy bloggers, Phil Plait aka the “Bad Astronomer” explains here. Also, I really enjoy this piece from the Jet Propulsion Laboratory's “Ask an Astronomer” series).  But I feel like most of the explanations that I have found lack a key piece of information, as I will explain below. The answer to this question has as much to do with human vision as it does astrophysics!

First, the basics. Hot objects emit light. Actually, "objects" of any temperature emit light in a very particular way that depends on their temperature. An idealization we use in physics is called the "blackbody", which basically is just an ideal object that absorbs all light/radiation that is incident upon it. The spectrum of light emitted by a blackbody is characterized by an equation called the Planck function. Using the Planck function you can find out how much light energy is emitted at every wavelength. The plot above shows Planck functions for three different temperatures: 4500 K, 5800 K, and 7500 K. I've also shown the region of the visual EM spectrum. Radiation that is shortward of about 390 nm is ultraviolet light (more violet than violet) and radiation that is longward of about 750 nm is infrared (redder than red). Human eyes are only sensitive to radiation in the colored portion of the plot.  

 Stars are basically really hot dense balls of mostly ionized hydrogen and helium gas. Blackbodies approximate the spectra of hot stars (and the hotter the star is the better a job the blackbody does, this is due to the relative absence of atomic and molecular absorption). This mean we can assign an "effective temperature" to a star based on its spectrum. For our Sun this temperature is about 5800 K. You can see that the Sun's blackbody spectrum peaks in the green part of the spectrum (more on this later)! So what's going on?

Well, consider what other objects act like blackbodies. Imagine a piece of iron a blacksmith heats to successively higher temperature. At first the metal glows a dull red, then perhaps an orange, then a yellow, then white, and finally blue. No green! That metal transitions through all the temperatures in the figure above, the blackbody peaks at all the visual wavelengths. However, if we look at the blackbody function, when it peaks in the green it's also emitting radiation at all the other wavelengths as well - the combination appears to our eyes as white.

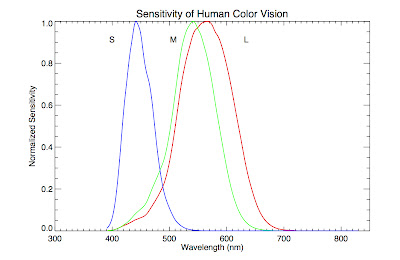
We can see why (beyond just waving our hands and saying "combining the colors in this ratio makes white") if we consider how humans perceive color. Our eyes contain specialized photoreceptor cells called cones that allow us to distinguish between different wavelength of light. There are three types of cones, labeled S, M, and L. They are sensitive to blue, green, and red light respectively. Our eye perceives colors other than blue, green, and red by interpolating between the input from these cone cells, in other words, taking into account the ratios of light detected by each one (e.g., orange is lots of red and a little green). Below is a plot of the relative sensitivity each cone cell has as a function of wavelength (data found here).

Notice that the green cone, M, overlaps substantially with the red cone, L, and somewhat with the blue one, S. In fact, it overlaps so substantially, and the blackbody function is so broad, that when a blackbody peaks in the middle of the visual spectrum, the combination appears white to our eyes. In truth, there is no temperature where there is substantial radiation in the green part of the spectrum and much less in the other parts.

So are we done now? Well, not quite. Remember that key piece of information I mentioned earlier that other authors hadn't considered? Here it is. Our eyes are not sensitive to the energy output of an object. In fact, neither are our telescopes or scientific instruments. What they are sensitive to, however, is photons. Photons are just little packets of light, and photons are what interact with the proteins in your eyes that register a visual signal. What's key to remember is that the amount of energy each photon carries is inversely proportional to its wavelength (and directly proportional to its frequency). 

There is a very important implication here. Since a photon with a longer wavelength carries less energy, at any given energy there are more photons at longer wavelengths. You can use this information to adjust the Planck function to give us a spectrum in terms of photon radiance rather than in terms of energy radiance. If you do this, the blackbody curve noticeable shifts and peaks in a different place. Below is another plot, of a 5800 K blackbody (e.g., representing the Sun). The solid line is in terms of energy and the dashed is in terms of photons.

Now instead of peaking in the green, the Sun peaks in the orange/red.  Of course, we are ignoring the wavelength sensitivity of the human eye here. If we convolved (combined) that sensitivity with the blackbody, we'd probably shift the peak back to shorter wavelengths a bit, but not nearly to green.  Notice also that the shape of the blackbody is flatter near the peak in terms of photons, making it less strongly peaked and easier to explain the "whiteness" of stars like the Sun. 

So, some people like to say the Sun is green in many respects, but this isn't really true. It's only true in terms of energy emitted at a given wavelength, which eyes and instruments don't measure. We only get the energy radiance by measuring photons and converting to energy by knowing how much energy each photon carries.

In summary, there are no green stars because the blackbody function is very broad, and the cone cell responsible for sensing green overlaps substantially with the other two cones cells. The Sun's blackbody function peaks in the green, but only in terms of energy, not photons, which are what our eyes actually detect.

In a second, follow up, post I will try to determine the "greenest" actual blackbody temperature, in terms of photon brightness, using the sensitivity function of the cone cells. Stay tuned!

Technical notes: You can determine the exact wavelength where a blackbody peaks by using an equation called Wien's Displacement Law, which is derived from the Planck function. There is a different Displacement Law for the peak (energy) radiation in terms of wavelength and frequency. Interestingly, the Sun's blackbody peak is even further into the red when using the frequency version of Wien's Law than in terms of photon flux. Actually, the photon peak is the 'compromise' value between the wavelength and frequency versions of Wien's Law.

*Some people claim that they do see a green star or two in the sky. More on that in a second post!